Los integrantes del Grupo

Alto paint deberian darme un premio

 Diaz Edgardo

 Agustin Bogdanich

Facundo Arrieta

Análisis de borde

Condiciones en la frontera entre dos materiales
distintos
Cuando dos diel´ectricos est´an en contacto a trav´es de una superficie S, se
plantea un problema, pues la superficie no pertenece propiamente a ninguno (no
est´a definida su permitividad) y hay una discontinuidad en ella. Para resolver
este problema, se recurre al teorema de Gauss, como veremos a continuaci´on.
Consideraremos aqu´ı solamente una situaci´on est´atica.
Sean dos medios 1 y 2, en contacto a trav´es de una superficie, con permitividades
1 y 2, tal como indica la figura, siendo n la normal a la superficie de
contacto, dirigida del medio 1 al 2. Tomemos la superficie S, un cilindro con bases
de ´area a, cada una en uno de los medios, y apliquemos el teorema de Gauss
al vector desplazamiento D, suponiendo que en la superficie de contacto hay una
densidad de cargas libres .
Z
D · n da = (D2 · n − D1 · n) a = a,
o sea
(D2 − D1) · n = . (1.15)
Por tanto, si hay densidad de cargas libres en la superifice de contacto, la componente
normal del vector desplazamiento tiene una discontinuidad.
Consideremos ahora el rect´angulo de la figura, con dos lados paralelos a la
superficie de contacto y dos de longitud despreciable perpendiculares a ella. Sean
t el vector unitario tangente a la superficie de contacto en el plano del rect´angulo.
Aplicando el teorema de Stokes a la circulaci´on del vector E, resulta
(E2 − E1) · t = 0,
notas EM II (v. 1/diciembre/2006) — Antonio Fern´
andez-Ra˜
nada 2006 —
1–3
Cap´ıtulo 1. Recordatorio de las ecuaciones de Maxwell
y como el vector t es arbitrario en el plano tangente a la superficie de contacto
(E2 − E1) × n = 0. (1.16)
Como vemos, la componente tangencial del campo el´ectrico es continua, con independencia
de que existan o no cargas el´ectricas libres en la superficie.
Conviene a veces plantear esta cuesti´on en t´erminos del potencial . Las
ecuaciones (1.15) y (1.16) se pueden escribir como
2
@
@n

2
− 1
@
@n

1
= , (1.17)
@
@t

2
−
@
@t

1
= 0, (1.18)
donde @n y @t son las derivadas seg´un la normal a la superficie y seg´un una
tangente. La segunda establece que, salvo una constante aditiva en uno de los dos
potenciales,
1 = 2
a lo largo y ancho del contacto.
Veamos qu´e ocurre con el vector polarizaci´on. Un razonamiento an´alogo al
hecho para el vector desplazamiento, nos lleva a
(P2 − P1) = − P .
Si 2 es el vac´ıo, P2 = 0, con lo que
P = P · n,
como cab´ıa esperar.
Consideremos ahora la frontera entre dos medios sometidos a un campo
magn´etico. Tomemos una superficie tipo p´ıldora, es decir un cilindro de peque˜na
altura, con eje perpendicular a la frontera y con una base en cada medio. Aplicando
el teorema de Gauss, se tiene que
(B2 − B1) · n = 0, o sea B2n − B1n = 0. (1.19)
La componente normal de B es continua en una frontera.
Sea ahora un circuito C en forma de rect´angulo, con dos lados de longitud
` y paralelos al vector t, tangente a la superficie, y los otros dos muy cortos y
normales a ella, suponiendo que circula por S una densidad superficial de corriente
1–4
— Antonio Fern´andez-Ra˜nada 2006 —
notas EM II (v. 1/diciembre/2006)
1.3. Condiciones en la frontera entre dos materiales distintos
k (cantidad de corriente por unidad de longitud normal a ella). Calculando la
circulaci´on del vector intensidad magn´etica H a lo largo de C, resulta
(H2 · `t − H1 · `t) = |k × `t|, o sea H2t − H1t = |k × t| ,
siendo k es la densidad superficial de corriente (o sea la corriente transportada
or unidad de longitud perpendicaula en la capa superficial). Como t es un vector
tangente arbitrario, se tiene
(H2 − H1) × n = k. (1.20)
O sea: si no hay carga libre superficial, la componente tangencial de H es continua.

Ondas incidente,reflejada y transmitida

n movimiento ondulatorio que incide sobre la superficie que separa dos medios de distintas propiedades mecánicas, ópticas, etc., en parte se refleja y en parte se transmite.
La velocidad de propagación de las ondas cambia al pasar de un medio a otro, pero no cambia la frecuencia angular w.
Supongamos que un movimiento ondulatorio se propaga a lo largo de dos cuerdas, la cuerda de la izquierda tiene una densidad lineal m₁ y la cuerda de la derecha tiene una densidad lineal m₂.

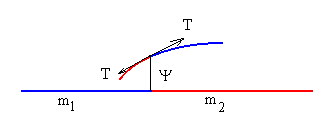
El movimiento ondulatorio transversal se propaga en ellas con velocidades, respectivamente, de

Siendo T la tensión de las cuerdas.

Ondas incidente, reflejada y trasmitida

Situamos el origen en el punto de unión de las cuerdas. A la izquierda del origen tenemos una onda armónica incidente cuyo número de onda es k₁ tal que k₁v₁=w , que se propaga de izquierda a derecha.
Y_i=Y_0i·sen (w t-k₁x)
y una onda reflejada que se propaga con la misma velocidad de derecha a izquierda
Y_r=Y_0r·sen (w t+k₁x)
Y=Y₀·sen (w t-kx) es una forma alternativa de expresar la ecuación de una onda armónica conveniente para este ejemplo.
En la segunda cuerda, tenemos una onda transmitida que se propaga de izquierda a derecha y cuyo número de onda es k₂ tal que k₂v₂=w .
Y_t=Y_0t·sen (w t-k₂x)
A la izquierda del origen, tenemos la superposición de dos movimientos ondulatorios, el incidente más el reflejado, Y₁=Y _i+Y _r
A la derecha del origen, solamente tenemos movimiento ondulatorio correspondiente a la onda transmitida, Y₂=Y _t

Relación entre las amplitudes de la onda incidente, reflejada y trasmitida

En el punto de discontinuidad o de unión de ambas cuerdas, el origen, x=0, el desplazamiento vale Y₁=Y₂, es decir
Y_0i·sen (w t)+Y_0r·sen (w t)=Y_0t·sen (w t)
Simplificando
Y_0i+Y_0r=Y_0t
Al estudiar las ondas transversales en una cuerda obtuvimos la expresión de la fuerza vertical F_y en cualquier punto de la cuerda.

La fuerza F_y en cualquier punto de la cuerda cuando se propaga una onda armónica es

En el origen x=0 se cumple
k₁(-Y_0i+Y_0r)=-k₂Y_0t
Desde el punto de vista matemático decimos, que en el punto de discontinuidad situado en el origen, la función que describe el movimiento ondulatorio debe ser continua y también  lo debe ser su derivada primera. Una situación análoga la encontraremos en Mecánica Cuántica al estudiar el escalón de potencial.
Tenemos dos ecuaciones, que nos permiten relacionar la amplitud de la onda reflejada Y_0r y transmitida Y_0t en términos de la amplitud de la onda incidente Y_0i

Expresando el número de onda k₁ y k₂ en términos de las velocidades de propagación respectivas v₁ y v₂
 

Actividades

En el siguiente applet se representan dos cuerdas unidas en el origen. En la primera región de color blanco, tenemos la superposición Y₁ del movimiento ondulatorio incidente, y reflejado dibujados en una línea de color azul. En la segunda región de color rosa, tenemos el movimiento ondulatorio transmitido Y₂ dibujado por una línea de color azul. Podemos observar que en el punto de discontinuidad, el origen, la función que describe el movimiento ondulatorio es continua y también su derivada primera.
Asimismo, se representa en la región de la izquierda, el movimiento ondulatorio incidente y reflejado, en los colores que se indican en la parte inferior del applet.
Observamos que la onda transmitida siempre está en fase con la onda incidente. Sin embargo, la onda reflejada puede estar en fase o en oposición de fase dependiendo de que la velocidad de propagación en el segundo medio v₂ sea mayor que en el primero v₁ o al contrario.

---

Se introduce

• La frecuencia del movimiento ondulatorio, en el control de edición titulado Frecuencia. Esta magnitud no cambia al propagarse un mismo movimiento ondulatorio por distintas medios.
• La velocidad de propagación de las ondas en el medio1 (a la izquierda), en el control de edición titulado V. medio1
• La velocidad de propagación de las ondas en el medio2 (a la derecha), en el control de edición titulado V. medio2

Se pulsa el botón titulado Empieza
Se pulsa el botón titulado Pausa para detener momentáneamente la animación y medir las longitudes de onda de la onda incidente, reflejada y trasmitida. Se pulsa el mismo botón titulado ahora Continua, para proseguir la animación. Se pulsa repetidamente el botón titulado Paso para acercar los nodos de la onda a las divisiones de la regla horizontal, a fin de medir su longitud de onda.

Experimento de Young

El experimento de Young, también denominado experimento de la doble rendija, fue realizado en 1801 por Thomas Young, en un intento de discernir sobre la naturaleza corpuscular u ondulatoria de la luz. Young comprobó un patrón de interferencias en la luz procedente de una fuente lejana al difractarseen el paso por dos rejillas, resultado que contribuyó a la teoría de la naturaleza ondulatoria de la luz.

Relevancia física

Posteriormente, la experiencia ha sido considerada fundamental a la hora de demostrar la dualidad onda corpúsculo, una característica de la mecánica cuántica. El experimento también puede realizarse con electrones, protones o neutrones, produciendo patrones de interferencia similares a los obtenidos cuando se realiza con luz.Aunque este experimento se presenta habitualmente en el contexto de la mecánica cuántica, fue diseñado mucho antes de la llegada de esta teoría para responder a la pregunta de si la luz tenía una naturaleza corpuscular o si, más bien, consistía en ondas viajando por el éter, análogamente a las ondas sonoras viajando en el aire. La naturaleza corpuscular de la luz se basaba principalmente en los trabajos de Newton. La naturaleza ondulatoria, en los trabajos clásicos de Hooke y Huygens.

Los patrones de interferencia observados restaban crédito a la teoría corpuscular. La teoría ondulatoria se mostró muy robusta hasta los comienzos delsiglo XX, cuando nuevos experimentos empezaron a mostrar un comportamiento que sólo podía ser explicado por una naturaleza corpuscular de la luz. De este modo el experimento de la doble rendija y sus múltiples variantes se convirtieron en un experimento clásico por su claridad a la hora de presentar una de las principales características de la mecánica cuántica.

La forma en la que se presenta normalmente el experimento no se realizó sino hasta 1961 utilizando electrones y mostrando la dualidad onda-corpúsculo de las partículas subatómicas (Claus Jönsson, Zeitschrift für Physik, 161, 454; Electron diffraction at multiple slits, American Journal of Physics, 42, 4-11, 1974). En 1974 fue posible realizar el experimento en su forma más ambiciosa, electrón a electrón, comprobando las hipótesis mecanocuánticas predichas por Richard Feynman. Este experimento fue realizado por un grupo italiano liderado por Pier Giorgio Merli y repetido de manera más concluyente en 1989por un equipo japonés liderado por Akira Tonomura y que trabajaba para la compañía Hitachi. El experimento de la doble rendija electrón a electrón se explica a partir de la interpretación probabilística de la trayectoria seguida por las partículas.

[editar]El experimento

[editar]Formulación clásica

La formulación original de Young es muy diferente de la moderna formulación del experimento y utiliza una doble rendija. En el experimento original un estrecho haz de luz, procedente de un pequeño agujero en la entrada de la cámara, es dividido en dos por una tarjeta de una anchura de unos 0.2 mm. La tarjeta se mantiene paralela al haz que penetra horizontalmente es orientado por un simple espejo. El haz de luz tenía una anchura ligeramente superior al ancho de la tarjeta divisoria por lo que cuando ésta se posicionaba correctamente el haz era dividido en dos, cada uno pasando por un lado distinto de la pared divisoria. El resultado puede verse proyectado sobre una pared en una habitación oscurecida. Young realizó el experimento en la misma reunión de la Royal Society mostrando el patrón de interferencias producido demostrando la naturaleza ondulatoria de la luz.

[editar]Formulación moderna

La formulación moderna permite mostrar tanto la naturaleza ondulatoria de la luz como la dualidad onda-corpúsculo de la materia. En una cámara oscura se deja entrar un haz de luz por una rendija estrecha. La luz llega a una pared intermedia con dos rendijas. Al otro lado de esta pared hay una pantalla de proyección o una placa fotográfica. Cuando una de las rejillas se cubre aparece un único pico correspondiente a la luz que proviene de la rendija abierta. Sin embargo, cuando ambas están abiertas en lugar de formarse una imagen superposición de las obtenidas con las rendijas abiertas individualmente, tal y como ocurriría si la luz estuviera hecha de partículas, se obtiene una figura de interferencias con rayas oscuras y otras brillantes.

Este patrón de interferencias se explica fácilmente a partir de la interferencia de las ondas de luz al combinarse la luz que procede de dos rendijas, de manera muy similar a como las ondas en la superficie del agua se combinan para crear picos y regiones más planas. En las líneas brillantes la interferencia es de tipo "constructiva". El mayor brillo se debe a la superposición de ondas de luz coincidiendo en fase sobre la superficie de proyección. En las líneas oscuras la interferencia es "destructiva" con prácticamente ausencia de luz a consecuencia de la llegada de ondas de luz de fase opuesta (la cresta de una onda se superpone con el valle de otra).

[editar]La paradoja del experimento de Young

Esta paradoja trata de un experimento mental, un experimento ficticio no realizable en la práctica, que fue propuesto por Richard Feynman examinando teóricamente los resultados del experimento de Young analizando el movimiento de cada fotón.

Para la década de 1920, numerosos experimentos (como el efecto fotoeléctrico, el efecto Compton, y la producción de rayos x entre otros) habían demostrado que la luz interacciona con la materia únicamente en cantidades discretas, en paquetes "cuantizados" o "cuánticos" denominados fotones. Si la fuente de luz pudiera reemplazarse por una fuente capaz de producir fotones individualmente y la pantalla fuera suficientemente sensible para detectar un único fotón, el experimento de Young podría, en principio, producirse con fotones individuales con idéntico resultado.

Si una de las rendijas se cubre, los fotones individuales irían acumulándose sobre la pantalla en el tiempo creando un patrón con un único pico. Sin embargo, si ambas rendijas están abiertas los patrones de fotones incidiendo sobre la pantalla se convierten de nuevo en un patrón de líneas brillantes y oscuras. Este resultado parece confirmar y contradecir la teoría ondulatoria de la luz. Por un lado el patrón de interferencias confirma que la luz se comporta como una onda incluso si se envían partículas de una en una. Por otro lado, cada vez que un fotón de una cierta energía pasa por una de las rendijas el detector de la pantalla detecta la llegada de la misma cantidad de energía. Dado que los fotones se emiten uno a uno no pueden interferir globalmente así que no es fácil entender el origen de la "interferencia".

La teoría cuántica resuelve estos problemas postulando ondas de probabilidad que determinan la probabilidad de encontrar una partícula en un punto determinado, estas ondas de probabilidad interfieren entre sí como cualquier otra onda.

Un experimento más refinado consiste en disponer un detector en cada una de las dos rendijas para determinar por qué rendija pasa cada fotón antes de llegar a la pantalla. Sin embargo, cuando el experimento se dispone de esta manera las franjas desaparecen debido a la naturaleza indeterminista de la mecánica cuántica y al colapso de la función de onda.

[editar]Condiciones para la interferencia

Las ondas que producen interferencia han de ser "coherentes", es decir los haces provenientes de cada una de las rendijas han de mantener una fase relativa constante en el tiempo, además de tener la misma frecuencia, aunque esto último no es estrictamente necesario, puesto que puede hacerse el experimento con luz blanca. Además, ambos han de tener polarizaciones no perpendiculares. En el experimento de Young esto se consigue al hacer pasar el haz por la primera rendija, produciendo una mutilación del frente de onda en dos frentes coherentes. También es posible observar franjas de interferencia con luz natural. En este caso se observa un máximo central blanco junto a otros máximos laterales de diferentes colores. Más allá, se observa un fondo blanco uniforme. Este fondo no está formado realmente por luz blanca, puesto que si, fijada una posición sobre la pantalla, se pone paralelo a la franja un espectrómetro por el cual se hace pasar la luz, se observan alternadamente franjas oscuras y brillantes. Esto se ha dado en llamar espectro acanalado. Las dos rendijas han de estar cerca (unas 1000 veces la longitud de onda de la luz utilizada) o en otro caso el patrón de interferencias sólo se forma muy cerca de las rendijas. La anchura de las rendijas es normalmente algo más pequeña que la longitud de onda de la luz empleada permitiendo utilizar las ondas como fuentes puntuales esféricas y reduciendo los efectos de difracción por una única rendija.

[editar]Resultados observados

Se puede formular una relación entre la separación de las rendijas, s, la longitud de onda λ, la distancia de las rendijas a la pantalla D, y la anchura de las bandas de interferencia (la distancia entre franjas brillantes sucesivas), x

λ / s = x / D

Esta expresión es tan sólo una aproximación y su formulación depende de ciertas condiciones específicas. Es posible sin embargo calcular la longitud de onda de la luz incidente a partir de la relación superior. Si s y D son conocidos y x es observado entonces λ puede ser calculado, lo cual es de especial interés a la hora de medir la longitud de onda correspondiente a haces de electrones u otras partículas.

Efecto Doppler sonoro

<!--[if lt IE 7]><![endif]

¿ Has notado cómo el tono de las sirenas de las ambulancias, de los bomberos o de la policía, cambia a medida que el auto se nos acerca?. La frecuencia es mayor a medida que el auto se nos acerca, luego, cambia súbitamente a una frecuencia menor a medida que se aleja. Este fenómeno es conocido como el Efecto Doppler. (La frecuencia es el número de vibraciones completas por segundo medidas en una posición fija).

                                 

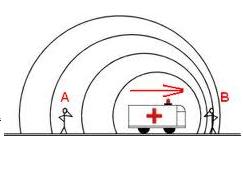 En este dibujo se puede ilustrar este efecto. La fuente sonora se mueve hacia la derecha, con una cierta velocidad, emitiendo ondas que se propagan en círculos centrados en la posición de la fuente (los observadores están ubicados uno adelante y otro atrás de la fuente en el momento que se generan las ondas.)

La frecuencia de la fuente sonora no cambia, pero cuando la fuente se acerca hacia el observador de adelante, más ondas se acumulan entre ellos. La longitud de onda se acorta. Aunque la velocidad del sonido no cambia, la frecuencia del sonido detectado aumenta.

En cambio, cuando la fuente se aleja del detector (de la persona que está detrás), la longitud de onda aumenta y la frecuencia detectada es menor. El efecto Doppler también se presenta si la fuente se encuentra estacionaria, y el detector está en movimiento.

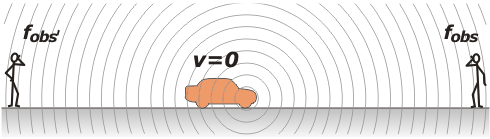Si la fuente emisora está detenida (sin movimiento) ambos observadores percibirán la misma frecuencia en la misma longitud de onda.

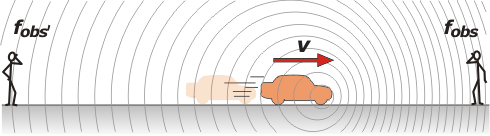Si la fuente emisora se mueve hacia adelante las ondas se juntan (se acortan) aumentando la frecuencia. Para el observador de atrás, las ondas se alargan (se separan), disminuyendo la frecuencia.

Aplicaciones del Efecto Doppler

El efecto Doppler posee muchas aplicaciones. Los detectores de radar lo utilizan para medir la rapidez de los automóviles y de las pelotas en varios deportes.

Los astrónomos utilizan el efecto Doppler de la luz  de galaxias distantes para medir su velocidad y deducir su distancia.

Los médicos usan fuentes de ultrasonido para detectar las palpitaciones del corazón de un feto; los murciélagos lo emplean para detectar y cazar a un insecto en pleno vuelo. Cuando el insecto se mueve más rápidamente que el murciélago, la frecuencia reflejada es menor, pero si el murciélago se está acercando al insecto, la frecuencia reflejada es mayor.

Ir a: Efecto Doppler: Fórmulas y cálculos

Para ver una animación del Efecto Doppler, ir a:

http://www.cimat.mx/~gil/tcj/2001/astronomia/hubble/doppler.html

Colocar el cursor en un punto cualquiera de la pantalla y hacer clic: el efecto Doppler se desplegará para saber cómo percibe el sonido alguien ubicado en ese punto.

Principio de Huygens

El principio de Huygens nos dice que todo punto alcanzado por una onda se comporta como un emisor de ondas.

Basándose en este principio y utilizando un método geométrico Huygens explicó perfectamente las propiedades de las ondas. (Reflexión, refracción, difracción e interferencias)

Representó las ondas mediante frentes de ondas ( conjunto de puntos consecutivos que están en fase) y rayos (rectas que indican la dirección de la propagación)

En 1678 Huygens propuso la naturaleza ondulatoria de la luz explicando mediante frentes de onda y rayos la propagación y las propiedades de la luz, en contraposición a la teoría corpuscular de Newton. 

Para ver una animación que explica  la reflexión y la refracción mediante el principio de Huygens pulsa el siguiente botón:

Este applet constituye un tutorial sencillo que explica la Reflexión y Refracción de Ondas mediante el Principio de Huygens. Las explicaciones para cada uno de los pasos (etapas) sucesivos van apareciendo en el cuadro de texto. Cuando se termina un paso, pulse el botón "Siguiente Paso". Puede pararse o reanudar la simulación mediante el botón "Pausa / Reanuda". Hay tres campos para texto donde pueden variarse los valores de los índices de refracción así como el ángulo de incidencia (recordar pulsar retorno de carro para aceptar el valor entrado). El medio con menor índice de refracción (mayor velocidad de fase) se visualiza en amarillo y el otro en azul.

Para ver el applet has click Aqui

Vector de Poynting

Vector de Poynting

El vector de Poynting es un vector cuyo modulo representa la intensidad instantánea de energía electromagnética que fluye a través de una unidad de área superficial perpendicular a la dirección de propagación de la onda y cuya dirección es la de propagación de la onda electromagnética. De una manera más general el vector de Poynting puede definirse como el producto vectorial del campo eléctrico y el campo magnético y cuyo módulo nos da la intensidad de la onda. Recibe su nombre del físico inglés John Henry Poynting y se expresa mediante el símbolo: .

 representa el campo eléctrico y  intensidad del campo magnético y  el campo de inducción magnética, siendo  la permeabilidad magnética del medio. Sus unidades en el SI son los Vatios sobre metro cuadrado.

Dado que los campos eléctrico y magnético de una onda electromagnética oscilan con la frecuencia de la onda, la magnitud del vector de Poynting cambia en el tiempo. El promedio del vector de Poynting sobre un período muy superior al periodo de la onda es llamado irradiancia, I:

.

La irradiancia representa el flujo de energía asociado a la radiación electromagnética en la dirección perpendicular a su dirección de propagación.